数据结构篇：二叉树

二叉树的创建，递归遍历及其他基础知识

二叉树的相关概念

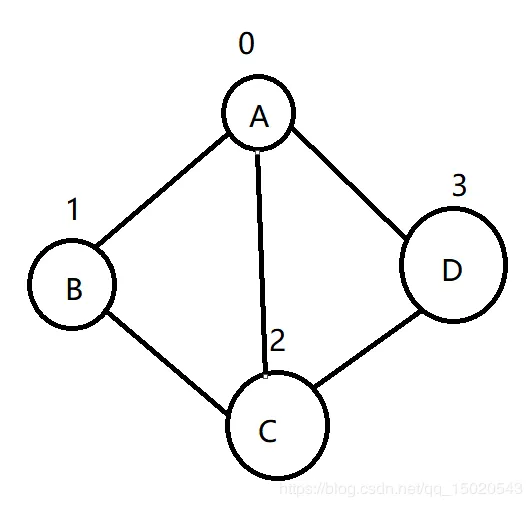
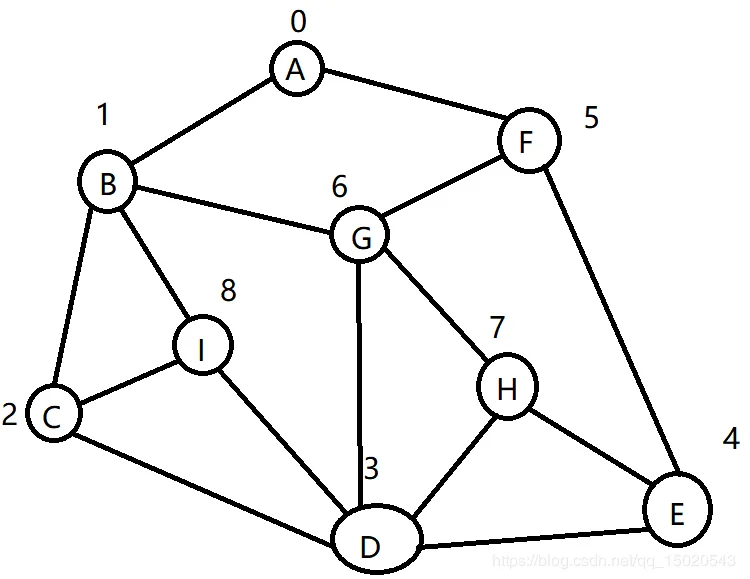
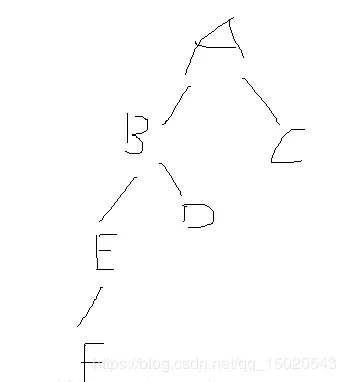
结点的度。结点所拥有的子树的个数称为该结点的度。例如右图B结点度数为2
叶结点。度为0的结点称为叶结点，或者称为终端结点。例如右图的F,D,C结点
分枝结点。度不为0的结点称为分支结点，或者称为非终端结点。一棵树的结点除叶结点外，其余的都是分支结点。例如右图的A,B,E，左图的A,B
结点的层数。规定树的根结点的层数为1，其余结点的层数等于它的双亲结点的层数加1。例如右图的F结点层数为4
树的深度（高度）。树中所有结点的最大层数称为树的深度。例如右图深度为4
树的度。树中各结点度的最大值称为该树的度。一般情况下，二叉树的度都为2

先给出结构

 struct BiTree 
{
    char data;
    BiTree *lchild,*rchild;
};

二叉树的创建

只能用先序法创建，单独的中序或后序都无法进行创建，原因和解决办法我会在以后博客进行完成

 BiTree * Tree :: PreCreateBiTree() 
 {
    BiTree *T;
    char c;
    cin>>c;
    if(c=='#') 
    {
        T=NULL;
    }
    else 
    {
        T=new BiTree;
        if(!T) 
        {
            cout<<"请求内存失败。"<<endl;
        } 
        else 
        {
            T->data=c;
        }
        T->lchild=PreCreateBiTree();
        T->rchild=PreCreateBiTree();
    }
    return T;
}

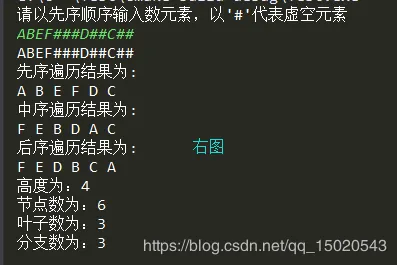
二叉树深度左图 3 右图 4

 int Tree::HeightOfthis(BiTree *T)
 {
    if(!T) return 0;
    else
    {
        return HeightOfthis(T->lchild)>HeightOfthis(T->rchild)?HeightOfthis(T->lchild)+1:HeightOfthis(T->rchild)+1;
    }
}

二叉树结点数左图 4 右图 6

 int Tree :: NodeOfthis(BiTree *T)
 {
    if(!T) return 0;
    else 
    {
        return 1+NodeOfthis(T->lchild)+NodeOfthis(T->rchild);
    }
}

二叉树叶子数（即没有分支结点的结点）左图 2 右图 3

 int Tree :: LeafOfthis(BiTree *T) 
 {
    if(!T) 
    {
        return 0;
    } 
    else if
    ((T->lchild == NULL) && (T->rchild == NULL)) 
    {
        return 1;
    } 
    else 
    {
        return  (BranchOfthis(T->lchild) + BranchOfthis(T->rchild));
    }

}

二叉树分枝数左图 2 右图 3

 int Tree :: BranchOfthis(BiTree *T) 
 {
    if(!T) 
    {
        return 0;
    } 
    else if(  (T->lchild == NULL) && (T->rchild == NULL) ) 
    {
        return 0;
    } 
    else 
    {
        return (1+ BranchOfthis(T->lchild) + BranchOfthis(T->rchild));
    }

}

完整程序

#include <iostream>
#include <string.h>
using namespace std;

struct BiTree {
    char data;
    BiTree *lchild,*rchild;
};
class Tree {
        BiTree *pt;
    public :
        Tree() {
            pt=NULL;
        }
        BiTree * PreCreateBiTree();
        void PreOrderTraverse(BiTree *T);
        void InOrderTraverse(BiTree *T);
        void LastOrderTraverse(BiTree *T);
        int HeightOfthis(BiTree *T);
        int NodeOfthis(BiTree *T);
        int LeafOfthis(BiTree *T);
        int BranchOfthis(BiTree *T); 
};

BiTree * Tree :: PreCreateBiTree() {
    BiTree *T;
    char c;
    cin>>c;
    if(c=='#') {
        T=NULL;
    } else {
        T=new BiTree;
        if(!T) {
            cout<<"请求内存失败。"<<endl;
        } else {
            T->data=c;
        }
        T->lchild=PreCreateBiTree();
        T->rchild=PreCreateBiTree();
    }
    return T;
}

void Tree::PreOrderTraverse(BiTree *T) {
    if(!T) {
        return ;
    } else {
        cout<<T->data<<" ";
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}
void Tree::InOrderTraverse(BiTree *T) {
    if(!T) {
        return ;
    } else {
        InOrderTraverse(T->lchild);
        cout<<T->data<<" ";
        InOrderTraverse(T->rchild);
    }
}
void Tree::LastOrderTraverse(BiTree *T) {
    if(!T) {
        return ;
    } else {
        LastOrderTraverse(T->lchild);
        LastOrderTraverse(T->rchild);
        cout<<T->data<<" ";
    }
}

int Tree::HeightOfthis(BiTree *T) {
    if(!T) return 0;
    else {
        return HeightOfthis(T->lchild)>HeightOfthis(T->rchild)?HeightOfthis(T->lchild)+1:HeightOfthis(T->rchild)+1;
    }
}

int Tree :: NodeOfthis(BiTree *T) {
    if(!T) return 0;
    else {
        return 1+NodeOfthis(T->lchild)+NodeOfthis(T->rchild);
    }
}

int Tree :: LeafOfthis(BiTree *T) {
    if(!T) {
        return 0;
    } else if(  (T->lchild == NULL) && (T->rchild == NULL) ) {
        return 1;
    } else {
        return  (LeafOfthis(T->lchild) + LeafOfthis(T->rchild));
    }

}

int Tree :: BranchOfthis(BiTree *T) {
    if(!T) {
        return 0;
    } else if(  (T->lchild == NULL) && (T->rchild == NULL) ) {
        return 0;
    } else {
        return (1+ BranchOfthis(T->lchild) + BranchOfthis(T->rchild));
    }

}


int main() {
    Tree tree;
    BiTree *biTree;
    cout<<"请以先序顺序输入数元素，以'#'代表虚空元素"<<endl;
    biTree = tree.PreCreateBiTree();
    cout<<"先序遍历结果为: "<<endl;
    tree.PreOrderTraverse(biTree);
    cout<<endl;
    cout<<"中序遍历结果为: "<<endl;
    tree.InOrderTraverse(biTree);
    cout<<endl;
    cout<<"后序遍历结果为: "<<endl;
    tree.LastOrderTraverse(biTree);
    cout<<endl;
    cout<<"高度为："<<tree.HeightOfthis(biTree)<<endl;
    cout<<"节点数为："<<tree.NodeOfthis(biTree)<<endl;
    cout<<"叶子数为："<<tree.LeafOfthis(biTree)<<endl;
    cout<<"分支数为："<<tree.BranchOfthis(biTree)<<endl;
    return 0;
}

二叉树的非递归遍历

二叉树是一种非常重要的数据结构，很多其它数据结构都是基于二叉树的基础演变而来的。对于二叉树，有前序、中序以及后序三种遍历方法。因为树的定义本身就是递归定义，因此采用递归的方法去实现树的三种遍历不仅容易理解而且代码很简洁。而对于树的遍历若采用非递归的方法，就要采用栈去模拟实现。在三种遍历中，前序和中序遍历的非递归算法都很容易实现，非递归后序遍历实现起来相对来说要难一点。

前言：

示例代码建议大家学习思想，而不是生搬硬套。
程序中类似 stack<结构体*> s 这种形式为利用#include<stack>所实现的，如果自己写栈的话，Pop，Push，Top方法都要自己写。而且会麻烦许多。这里建议大家直接以这种形式写。
对于后序非递归遍历，三种结构体有着这样的关系。（以我文末的程序为例（栈自己编写））
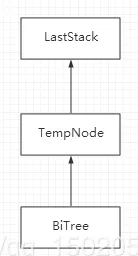
对于先序和中序，则没有中间那个带标识的结构体，直接就是栈。这同时也是建议大家使用stack<结构体*> s形式的理由，因为数据类型的不同，势必要改写Pop，Push，GetTop函数，很麻烦。
参考自https://www.cnblogs.com/SHERO-Vae/p/5800363.html

前序遍历

前序遍历按照“根结点-左孩子-右孩子”的顺序进行访问。根据前序遍历访问的顺序，优先访问根结点，然后再分别访问左孩子和右孩子。即对于任一结点，其可看做是根结点，因此可以直接访问，访问完之后，若其左孩子不为空，按相同规则访问它的左子树；当访问其左子树时，再访问它的右子树。因此其处理过程如下：对于任一结点P：

访问结点P，并将结点P入栈;
判断结点P的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点P，循环至1;若不为空，则将P的左孩子置为当前的结点P;
直到P为NULL并且栈为空，则遍历结束。

void TraTree::PreOrderTraverse(Tree *T)
{
    Tree *p = T;
    stack<Tree *> stack;
    cout << "非递归前序遍历：";
    while (p != NULL  !stack.empty())
    {
        while (p != NULL)
        {
            cout << p->data <<" ";
            stack.push(p);
            p = p->lchild;
        }

        if (!stack.empty())
        {
            p = stack.top();
            stack.pop();
            p = p->rchild;
        }
    }
    cout << endl;
}

中序遍历

中序遍历按照“左孩子-根结点-右孩子”的顺序进行访问。根据中序遍历的顺序，对于任一结点，优先访问其左孩子，而左孩子结点又可以看做一根结点，然后继续访问其左孩子结点，直到遇到左孩子结点为空的结点才进行访问，然后按相同的规则访问其右子树。因此其处理过程如下：对于任一结点P，

若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；
若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；
直到P为NULL并且栈为空则遍历结束。

void TraTree::InOrderTraverse(Tree *T)
{
    Tree *p = T;
    stack<Tree *> stack;
    cout << "非递归中序遍历：";
    while (p != nullptr  !stack.empty())
    {
        while (p != nullptr)
        {
            stack.push(p);
            p = p->lchild;
        }

        if (!stack.empty())
        {
            p = stack.top();
            cout << p->data << " ";
            stack.pop();
            p = p->rchild;
        }
    }
    cout << endl;
}

后序遍历

后序遍历按照“左孩子-右孩子-根结点”的顺序进行访问。后序遍历的非递归实现是三种遍历方式中最难的一种。因为在后序遍历中，要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点，这就为流程的控制带来了难题。下面介绍两种思路。对于任一结点P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问，因此其右孩子还为被访问。所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问。这样就保证了正确的访问顺序。可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。是为1，否为2.

void TraTree::LastOrderTraverse(Tree *T)
{
    Tree *p = T;
    TempTreeNode *temp;
    stack<TempTreeNode *> stack;
    cout << "非递归后序遍历：";
    while (p != nullptr  !stack.empty())
    {
        while (p != nullptr)
        {
            TempTreeNode *temp = new TempTreeNode;
            temp->tempNode = p;
            temp->tag = 1;
            stack.push(temp);
            p = p->lchild;
        }

        if (!stack.empty())
        {
            temp = stack.top();
            stack.pop();
            if (temp->tag == 1)
            {
                temp->tag = 2;
                stack.push(temp);
                p = temp->tempNode->rchild;
            }
            else
            {
                cout << temp->tempNode->data << " ";
                p = nullptr;
            }
        }
    }

}

完整代码

//
// Created by 烟雨迷离半世殇 on 2020/2/13.
//

#include <iostream>
#include <stack>

using namespace std;

//二叉树
typedef struct BiTree
{
    char data;
    BiTree *lchild, *rchild;
} Tree;

//后序非递归遍历需要为每个结点设置标识，所以新建一个结构体
typedef struct TempNode
{
    Tree *tempNode;
    int tag;
} TempTreeNode;

class TraTree
{
private :
    Tree *root;
public:
    TraTree()
    {
        root = nullptr;
    }

    Tree *PreCreateBiTree();//先序创立二叉树
    void PreOrderTraverse(Tree *T);//先序遍历
    void InOrderTraverse(Tree *T);//中序遍历
    void LastOrderTraverse(Tree *T);//后序遍历
};


Tree *TraTree::PreCreateBiTree()
{
    Tree *T;
    char c;
    cin >> c;
    if (c == '#')
    {
        T = NULL;
    }
    else
    {
        T = new Tree;
        T->data = c;
        T->lchild = PreCreateBiTree();
        T->rchild = PreCreateBiTree();
    }
    return T;
}

void TraTree::PreOrderTraverse(Tree *T)
{
    Tree *p = T;
    stack<Tree *> stack;
    cout << "非递归前序遍历：";
    while (p != NULL  !stack.empty())
    {
        while (p != NULL)
        {
            cout << p->data <<" ";
            stack.push(p);
            p = p->lchild;
        }

        if (!stack.empty())
        {
            p = stack.top();
            stack.pop();
            p = p->rchild;
        }
    }
    cout << endl;
}

void TraTree::InOrderTraverse(Tree *T)
{
    Tree *p = T;
    stack<Tree *> stack;
    cout << "非递归中序遍历：";
    while (p != nullptr  !stack.empty())
    {
        while (p != nullptr)
        {
            stack.push(p);
            p = p->lchild;
        }

        if (!stack.empty())
        {
            p = stack.top();
            cout << p->data << " ";
            stack.pop();
            p = p->rchild;
        }
    }
    cout << endl;
}

void TraTree::LastOrderTraverse(Tree *T)
{
    Tree *p = T;
    TempTreeNode *temp;
    stack<TempTreeNode *> stack;
    cout << "非递归后序遍历：";
    while (p != nullptr  !stack.empty())
    {
        while (p != nullptr)
        {
            TempTreeNode *temp = new TempTreeNode;
            temp->tempNode = p;
            temp->tag = 1;
            stack.push(temp);
            p = p->lchild;
        }

        if (!stack.empty())
        {
            temp = stack.top();
            stack.pop();
            if (temp->tag == 1)
            {
                temp->tag = 2;
                stack.push(temp);
                p = temp->tempNode->rchild;
            }
            else
            {
                cout << temp->tempNode->data << " ";
                p = nullptr;
            }
        }
    }

}

int main()
{
    TraTree traTree;
    Tree *tree;
    cout << "请以先序顺序输入数元素，以'#'代表虚空元素" << endl;
    tree = traTree.PreCreateBiTree();
    traTree.PreOrderTraverse(tree);
    traTree.InOrderTraverse(tree);
    traTree.LastOrderTraverse(tree);
    return 0;
}

根据中序和后序遍历结果推算出完整二叉树

我们先理解一下前中后序遍历，这是基础。

 //前序遍历
void Tree::PreOrderTraverse(BiTree *T) {
    if(!T) {
        return ;
    } else {
        cout<<T->data<<" ";
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

//中序遍历
void Tree::InOrderTraverse(BiTree *T) {
    if(!T) {
        return ;
    } else {
        InOrderTraverse(T->lchild);
        cout<<T->data<<" ";
        InOrderTraverse(T->rchild);
    }
}

//后序遍历
void Tree::LastOrderTraverse(BiTree *T) {
    if(!T) {
        return ;
    } else {
        LastOrderTraverse(T->lchild);
        LastOrderTraverse(T->rchild);
        cout<<T->data<<" ";
    }
}

我们理解到以下几点：

前序遍历是从一个根节点左子树开始遍历，同时输出，当左子树为空，就遍历右子树，右子树不为空就输出
中序遍历是从一个根节点左子树开始遍历，直到它的左子树为空，就输出，然后输出此根节点，然后遍历右子树，同理输出
后序遍历也是从一个根节点左子树开始遍历，直到它的左右子树都为空，就输出，然后遍历右子树，同理输出，最后输出根节点比如这个二叉树

我的分析方法是按照后序遍历的结果进行分块推算举个例子 二叉树的中序遍历CBEFDGAJILKHNOMP 后序遍历CFEGDBJLKIONPMHA 请推算出整个二叉树 1.先看后序遍历结果，A是最后一位，所以A就是顶点，然后A前一位是H，所以H为A的右子树顶点， 2.又由中序遍历结果，以A为分界点，将树分为两部分。 又由后序遍历结果，知B为A的左子树顶点 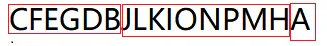所以目前为止我们的二叉树为 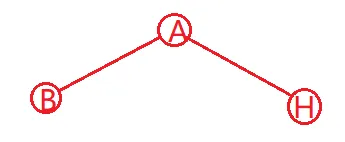3.从左子树开始分析 由中序遍历结果知，C为B的左子树顶点。D为B的右子树顶点 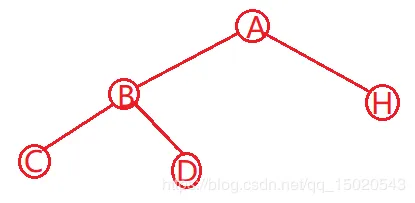继续同理分析，G为D的右子树顶点，而对于EF，中序遍历顺序为EF，后序遍历为FE，只有一种情况，E为F的双亲结点 且F为E的右子树顶点，因为如果F为E的左子树顶点，那么中序遍历的结果就是FE，而不是EF。至此，左子树推算完毕。 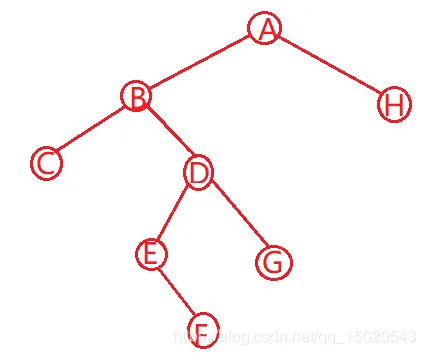4.然后是A的右子树 由中序遍历分析得，JILK为H的左子树部分，NOMP为H的右子树部分 先分析JILK，I为H的左子树顶点，M为H的右子树顶点 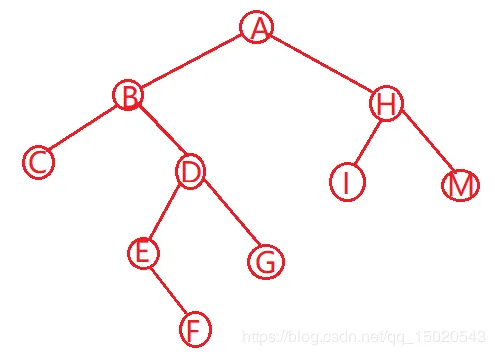由中序遍历知I的左子树为J，右子树为LK，并且对于LK，K为I的右子树顶点，L为K的左子树顶点，因为如果L为K的右子树顶点，中序遍历结果将是KL[toc] 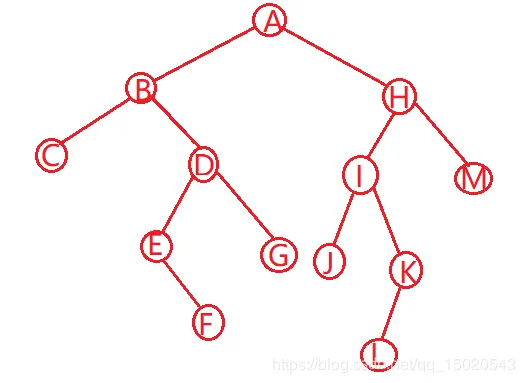再分析NOMP 由中序遍历，P为M的右子树顶点，NO为M的左子树部分，且中序遍历结果为NO，后序遍历结果为ON，所以N为M的左子树顶点，O为N的右子树顶点，所以有 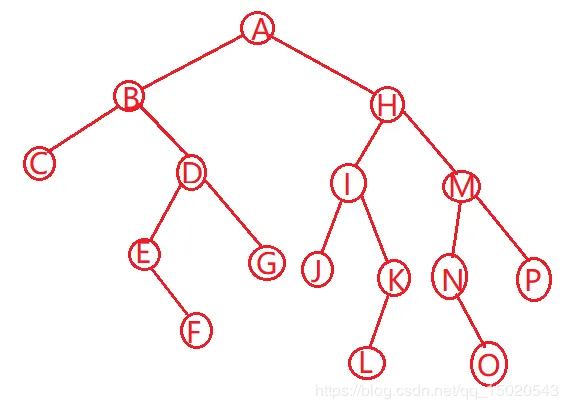至此二叉树已经完整的推算出来了。 可能看起来很复杂，但是大家在掌握后序遍历，中序遍历的基础上进行理解分析得话，还是比较容易掌握的。多多练习就好。

交换左右子树

应用递归思想如果结点不为空，就交换其左右子树，而待交换的左右子树，我们不需要关心是否为空。

 void Tree::ExChangeTree(BiTree *T) {

    BiTree *temp = new BiTree;
    if (T)
    {
        temp = T->rchild;
        T->rchild = T->lchild;
        T->lchild = temp;
        ExChangeTree(T->lchild);
        ExChangeTree(T->rchild);
    }
    else
    {
        return;
    }
}

运行截图完整程序

 //
// Created by 烟雨迷离半世殇 on 2018/11/28.
//

#include <iostream>
#include <string.h>

using namespace std;

struct BiTree {
    char data;
    BiTree *lchild, *rchild;
};

class Tree {
    BiTree *pt;
public :
    Tree() {
        pt = NULL;
    }

    BiTree *PreCreateBiTree();

    void PreOrderTraverse(BiTree *T);

    void InOrderTraverse(BiTree *T);

    void LastOrderTraverse(BiTree *T);

    void ExChangeTree(BiTree *T);
};

BiTree *Tree::PreCreateBiTree() {
    BiTree *T;
    char c;
    cin >> c;
    if (c == '#')
    {
        T = NULL;
    }
    else
    {
        T = new BiTree;
        if (!T)
        {
            cout << "请求内存失败。" << endl;
        }
        else
        {
            T->data = c;
        }
        T->lchild = PreCreateBiTree();
        T->rchild = PreCreateBiTree();
    }
    return T;
}

void Tree::PreOrderTraverse(BiTree *T) {
    if (!T)
    {
        return;
    }
    else
    {
        cout << T->data << " ";
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

void Tree::InOrderTraverse(BiTree *T) {
    if (!T)
    {
        return;
    }
    else
    {
        InOrderTraverse(T->lchild);
        cout << T->data << " ";
        InOrderTraverse(T->rchild);
    }
}

void Tree::LastOrderTraverse(BiTree *T) {
    if (!T)
    {
        return;
    }
    else
    {
        LastOrderTraverse(T->lchild);
        LastOrderTraverse(T->rchild);
        cout << T->data << " ";
    }
}

void Tree::ExChangeTree(BiTree *T) {

    BiTree *temp = new BiTree;
    if (T)
    {
        temp = T->rchild;
        T->rchild = T->lchild;
        T->lchild = temp;
        ExChangeTree(T->lchild);
        ExChangeTree(T->rchild);
    }
    else
    {
        return;
    }
}


int main() {
    Tree tree;
    BiTree *biTree;
    cout << "请以先序顺序输入数元素，以'#'代表虚空元素" << endl;
    biTree = tree.PreCreateBiTree();
    cout << "先序遍历结果为: " << endl;
    tree.PreOrderTraverse(biTree);
    cout << endl;
    cout << "中序遍历结果为: " << endl;
    tree.InOrderTraverse(biTree);
    cout << endl;
    cout << "后序遍历结果为: " << endl;
    tree.LastOrderTraverse(biTree);
    cout << "交换左右子树结果为: " << endl;
    tree.ExChangeTree(biTree);
    cout << "先序遍历结果为: " << endl;
    tree.PreOrderTraverse(biTree);
    cout << endl;
    cout << "中序遍历结果为: " << endl;
    tree.InOrderTraverse(biTree);
    cout << endl;
    cout << "后序遍历结果为: " << endl;
    tree.LastOrderTraverse(biTree);
    return 0;
}